Les principes de numération en informatique

I. Présentation

La numération, c'est le système qui permet de donner un nom aux nombres et aux systèmes qui permettent de compter. En informatique, on travaille avec des systèmes différents de celui des humains : binaire, hexadécimal, etc. Comprendre donc le fonctionnement des systèmes de numération va aider le débutant (et les moins débutants) à comprendre comment manipuler ces nombres étranges.

II. Principe de position

Dans notre système numérique « humain », nous comptons en base 10, appelé également le système décimal. Ce système, comme tout système numérique, comporte N chiffres allant de 0 à N-1 ; soit dans notre cas 10 chiffres allant de 0 à 9 (car oui, le zéro compte !).

Afin de continuer à compter au-delà des unités, nous utilisons un système de position des chiffres. Une fois les unités épuisées, nous ajoutons une position supplémentaire (dizaine) nous permettant de signifier le passage à un autre niveau.

Prenons le nombre décimal 5469, il est composé de :

• 9 unités
• 6 dizaines
• 4 centaines
• 5 milliers

Par décomposition, nous pouvons écrire :

• 5469 = (5 x 1000) + (4 x 100) + (6 x 10) + (9 x 1)

Ou encore :

• 5469 = (5x10³) + (4 x 10²) + (6 x 10¹) + (9 x 10⁰)

Dans ce dernier exemple, 10 représente la base (car nous sommes en base 10) et la puissance représente la position du chiffre composant le nombre :

3	2	1	0
5	4	6	9

Bien entendu, ces opérations, nous les faisons de manière automatique sans même se poser la question ni se rendre compte que nous les faisons, mais la compréhension de cette mécanique est très importante pour la suite de l'article.

III. Le "2" n'existe pas!

N’ayez pas peur du titre, je vous explique…

Nous humains, comme cité plus haut, comptons en base 10 pour la simple et bonne raison que… nous avons dix doigts !

Pour ceux que ça intéresse, les gaulois avaient un système en base 20, car si on compte les orteils de pied... On appelle cela le système vicésimal et on en conserve quelques traces dans notre langue (quatre-vingts, quatre-vingt-dix).

Mais, en informatique, cette notation devient complexe à mettre en œuvre d’un point de vue « machine ». D’une part, parce qu’elles n’ont pas de doigts, et d’autre part parce que cela demandera des temps de calcul beaucoup plus longs. En n’utilisant que 2 chiffres, les processeurs peuvent optimiser leurs ressources par une addition de calculs plus simples, donc plus rapides (je résume dans les grandes lignes).

Nous allons donc essayer de comprendre comment calcule un ordinateur, car c’est le fondement de la compréhension du réseau (et de bien d’autres domaines de l’informatique), notamment de l’adressage IP.

Ce système ne diffère en rien du précédent, en effet, il s’agit là encore d’un système à position, mais au lieu d’utiliser 10 chiffres, nous n’en utiliserons que 2 :

• 0 et 1

Oui, c'est tout ! Ces chiffres, que nous nommerons bits (pour Binary Digit) à partir de maintenant, sont l’unique base du système binaire, mais permettent de coder l’ensemble des chiffres de base 10.

Tout d’abord, revenons sur ce principe de position. Comme nous l’avons dit, une fois que les unités sont épuisées, nous ajoutons un chiffre à la position supérieure, exemple ici en base 10 avec 9+1 :

Et, c'est strictement identique en système binaire ! Si je commence à compter en binaire, cela donne ça :

Là, je n’ai plus rien à ajouter au niveau des unités, donc j’ajoute une unité à la position 1 :

Puis je passe à l’unité suivante :

Encore une fois, je n’ai pas de chiffre après le « 1 » donc je passe à la position suivante :

Et ainsi de suite… Voilà, vous savez compter en binaire ! Mais pour l’instant, ça ne veut pas dire grand-chose…

IV. Conversions inter-systèmes

Afin de bénéficier des avantages à comprendre le système binaire, il est indispensable de savoir réaliser les conversions d’un système à l’autre. Nous allons balayer les techniques existantes.

A. Méthode de la division

Prenons un nombre au hasard : 516

Nous allons diviser ce nombre par la quantité de valeur possible en système binaire, soit 2.

• Si le résultat de la division est un nombre à virgule, on note 1.

• Si le résultat de la division est un nombre juste, on note 0.

• La notation reprend ainsi les résultats obtenus de droite à gauche. Allons-y !

516/2 = 258 on note 0

258/2 = 129 on note 0

129/2 = 64,5 on note 1

64/2 = 32 on note 0

32/2 = 16 on note 0

16/2 = 8 on note 0

8/2 = 4 on note 0

4/2 = 2 on note 0

2/2 = 1 on note 0

1/2 = 0,5 on note 1

Maintenant, si on lit les valeurs binaires de bas en haut, cela donne 1000000100, soit 516 !

B. Méthode de la position

Comme nous l’avons indiqué, le système binaire est un système à position. Tout comme le système décimal, chaque position équivaut, la valeur N^p ou « p » est la position concernée. Nous pouvons ainsi écrire une table des valeurs binaires en fonction de leur position avec les puissances de 2 :

Note : tout nombre à la puissance 0 est égal à 1 !

Il suffit donc de faire ensuite une série de soustractions, reprenons 516 : 516 est supérieur à 512, je soustrais donc :

516 – 512 = 4, comme j’ai utilisé la valeur « 512 », je mets un « 1 » à la case correspondante :

4 est inférieur à 256, je ne fais rien et je mets « 0 » à la valeur

4 est inférieur à 128, je ne fais rien et je mets « 0 » à la valeur

Je ne détaille pas, vous avez compris le principe, 4 étant inférieur aux quatre autres valeurs, on inscrit "0" :

Ah, là ça devient intéressant, car 4 est égal à 4 ! 4 – 4 = 0 et je mets « 1 » à la valeur :

Comme j’arrive à « 0 », je sais que je n’aurai plus de valeur à soustraire, car mon stock est vide, donc je mets 0 dans les cases restantes :

Et, nous avons notre nombre 516 !

C. Conversion binaire vers décimal

Cette méthode de la position est également utile si on souhaite faire l’opération inverse. En effet, maintenant que l’on connaît les valeurs de chaque puissance de 2, il suffit de les additionner pour retrouver la valeur décimale d’un nombre binaire.

Exemple : prenons le nombre binaire 1010011, nous pouvons remplir notre tableau (en commençant par la droite) :

Si j’additionne les valeurs correspondantes aux Bits à « 1 », voici ce que j’obtiens : 64 + 16 + 2 + 1 = 83.

Et voilà, nous avons réalisé une conversion binaire /décimale ! Facile non ?

V. "F" est un nombre

Oui, vous avez bien lu et non, je ne suis pas devenu fou !

Maintenant que nous avons compris les bases du binaire, il nous reste à voir un autre système : l’hexadécimal.

Ce système de numération est en base 16. Le principe fondamental de l’utilisation d’une telle base est que les nombres binaires, pour nous humain, sont relativement longs, et donc difficiles à manipuler.

Le format hexadécimal a donc été créé sur la base de nos chiffres de base 10 auxquels ont été ajoutés les 6 premières lettres de l’alphabet. Donc si je compte en hexadécimal, voici ce que cela donne :

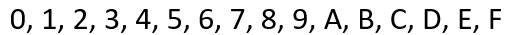
Ce système est une fois de plus un système à position ou chaque valeur vaut N^p. Exemple avec 3B8 : 8 x 16⁰ + 11 x 16¹ + 3 x 16² = 952

La conversion par ce biais n’est pas aisée, j’en conviens (sauf si vous connaissez vos puissances de 16...)

Pour les plus aiguisés d’entre vous, vous avez pu constater que « 16 » est une puissance de « 2 ». Super ! nous allons pouvoir utiliser le binaire, que nous connaissons maintenant sur le bout des doigts pour passer du décimal à l’hexadécimal et inversement.

Si nous reprenons notre tableau des valeurs des puissances de 2, on constate que 2⁴ = 16, donc à un chiffre de base 16 correspond 4 chiffres de base 2.

Reprenons notre exemple "3B8", nous savons maintenant qu’à chaque « partie » correspond 4 chiffres binaires :

Il suffit de convertir chaque chiffre en binaire (pour rappel, « B » vaut 11) et ça, vous savez le faire !

Les premiers « 0 » peuvent être omis dans la notation, nous avons donc le nombre binaire suivant : 1110111000.

Il ne nous reste plus qu’à le convertir en décimal selon notre tableau :

Soit 512 +256 + 128 + 32 + 16 + 8 = 952, le compte est bon !

Pour passer du décimal à l’hexadécimal, il suffit de réaliser l’opération inverse.

VI. Volumétrie

Maintenant que nous avons appris à compter, il faut impérativement que nous arrivions à quantifier.

Vous l’avez remarqué, nous n’utilisons que très peu la notion de « bits » lorsque nous utilisons un système d’exploitation contrairement au réseau. Comme les nombres sont très grands, il a fallu trouver un moyen de les regrouper en unité plus importante.

A. Système international

Vous le connaissez tous si vous avez déjà acheté ne serait-ce qu’une clé USB.

Pour faciliter la manipulation de grands nombres binaires, nous utilisons un regroupement par 8 : l’octet. Cette unité se note « o » (petit o) et vaut donc 8 bits. L’octet suit les normes du système international, qui régissent également les mesures de poids, de distance, etc. Nous avons donc le tableau des valeurs suivantes :

Nom	Octet	Kilo	Méga	Giga	Téra
Valeur en o	1	1000	1000000	1000000000	1000000000000

En anglais, une unité d’adressage est nommée Byte (B, que l’on traduit par multiplet en français), indépendamment de sa valeur réelle en bits, car dépendant, par exemple, du langage de programmation utilisé (en langage C un Byte vaut plus de 8 bits). Cependant, l’usage courant de l’unité d’adressage 8 bits dans les systèmes informatique a conduit à la normalisation suivante : 1 octet = 1 Byte = 8 bits.

C’est pour cela que selon le vendeur, une barrette de mémoire peut être vendue pour une capacité annoncée de 4 Go ou de 4 GB, mais c’est la même chose !

Revenons à notre système international, nous avons vu que pour manipuler de grandes quantités d’octets, nous utilisons des multiples de 10.

Mais attendez ! Il n’y a pas un problème ? Un bit est une valeur en base 2 non ?

B. Préfixe binaire

En 1999, la Commission électrotechnique internationale (CEI) a publié une nouvelle norme visant à rétablir une vérité : un octet valant 8 bits et un bit étant une valeur en base 2, la volumétrie devait en tenir compte. Ils ont donc créé les préfixes binaires en réutilisant les préfixes internationaux auxquels ont été ajoutés la syllabe « bi » : kibi, mébi, gibi, tébi, etc.

Ainsi, à l’instar d’un kilo-octet qui vaut 10³ octets soit 1000 octets un kibi octet vaut 2¹⁰ octets soit 1024 octets, logique, car nous sommes en base 2. Voici les valeurs de chaque unité :

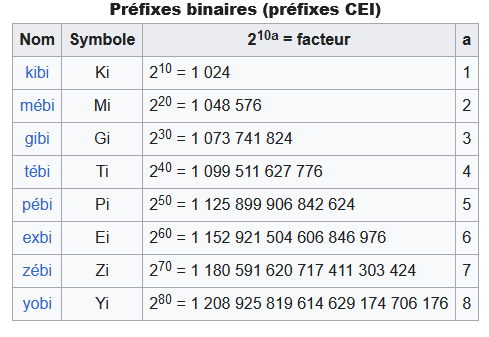
Cette nouvelle norme a créée une confusion chez les utilisateurs, alimentée par le mauvais usage de tel ou tel préfixe par les fabricants eux-mêmes, voire par les développeurs de systèmes d’exploitation.

Tout fabricant de disque dur ou de mémoire vous vendra une quantité de stockage en utilisant le système international. Le problème, c’est que mon système d’exploitation, lui, compte en base 2…

En effet, si je regarde dans les propriétés de mon disque dur (le mien fait 120 Go) :

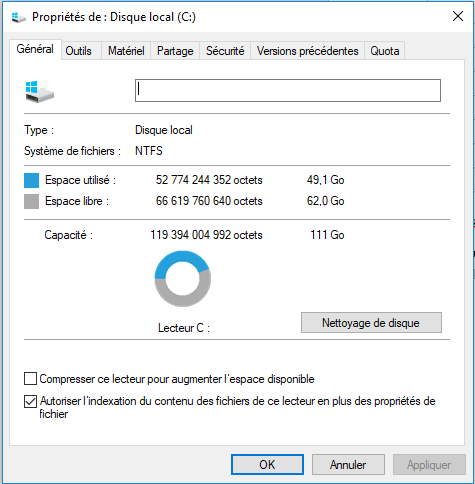
On peut constater que mon PC me dit qu’il ne fait que 111 Go ! Je me suis fait rouler !

En réalité non, c’est simplement que (pour une raison floue) Windows indique une valeur en Go alors qu’elle est exprimée en Gio !

Si je prends la capacité totale de mon disque dur tel qu’elle m’a été vendue par le marchand : 120 Go = 120 000 000 000 octets. Nous avons dit que 1 kio = 1024 octets.

• 120 000 000 000 / 1024 = 117 187 500 Kio
• 117 187 500 / 1024 = 114 440, 917 Mio
• 114 440,917 / 1024 = 111,76 Gio

SI j’arrondis, j’ai bien le même résultat que Windows !

SI vous souhaitez faire le calcul plus rapidement, il suffit de diviser la valeur en Go par 1,073 : 120/1.073 = 111,83 soit effectivement 111 en arrondissant.

Donc personne ne se fait rouler, nous ne parlons simplement pas avec la même unité ; un peu comme avec les degrés Celsius ou Fahrenheit, il n'y en a pas un qui est plus froid que l'autre !

Pour poursuivre votre apprentissage, consultez cet article :

• Le calcul de masque de sous-réseau avec l'adressage IPv4